|
5-1 單極發電機為一個在均勻磁場B中繞軸旋轉的金屬圓盤,圓盤的半徑為a,角速度為ω,圓盤與磁場垂直,求感應電動勢。
5-2 一個電荷Q,以恒定速度v(v<<c)沿半徑為a的圓形平面S的軸線向此平面移動,當兩者相距為d時,求通過S的位移電流。
5-3 假設電場是正弦變化的,海水的電導率為4S/m,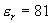 ,求當f=1MHz時,確定位移電流與傳導電流模的比值。
,求當f=1MHz時,確定位移電流與傳導電流模的比值。
5-4 一圓柱形電容器,內導體半徑為a,外導體半徑為b,長度為l,電極間介質的介電常數為ε。當外加低頻電壓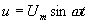 時,求介質中的位移電流密度及穿過半徑為r(a<r<b)的圓柱面的位移電流。證明此位移電流等于電容器引線中的傳導電流。
時,求介質中的位移電流密度及穿過半徑為r(a<r<b)的圓柱面的位移電流。證明此位移電流等于電容器引線中的傳導電流。
5-5 已知空氣媒質的無源區域中,電場強度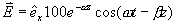 ,其中
,其中 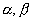 為常數,求磁場強度。 為常數,求磁場強度。
5-6 證明麥克斯韋方程組包含了電荷守恒定律。
5-7 證明媒質分界面上沒有自由面電荷和自由面電流(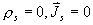 )時,分界面上只有兩個切向分量 的邊界條件是獨立的,法向分量的邊界條件已經包含在切向分量的邊界條件中。
)時,分界面上只有兩個切向分量 的邊界條件是獨立的,法向分量的邊界條件已經包含在切向分量的邊界條件中。
5-8 在兩導體平板(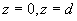 )之間的空氣中傳輸的電磁波,其電場強度矢量
)之間的空氣中傳輸的電磁波,其電場強度矢量
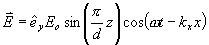
其中kx為常數。試求:(1)磁場強度矢量 ;(2)兩導體表面上的面電流密度
。
5-9 假設真空中的磁感應強度
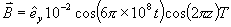
試求位移電流密度。
5-10 在理想導電壁(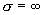 )限定的區域(
)限定的區域(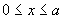 )內存在一個如下的電磁場:
)內存在一個如下的電磁場:
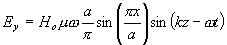
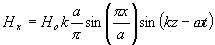
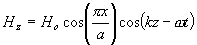
這個電磁場滿足的邊界條件如何?導電壁上的電流密度的值如何?
5-11 一段由理想導體構成的同軸線,內導體半徑為a,外導體半徑為b,長度為L,同軸線兩端用理想導體板短路。已知在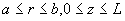 區域內的電磁場為
區域內的電磁場為
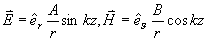
(1)確定A,B之間的關系。
(2)確定k。
(3)求r=a及r=b面上的 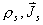 。 。
5-12 一根半徑為a的長直圓柱導體上通過直流電流I。假設導體的電導率σ―為有限值,求導體表面附近的坡印廷矢量,計算長度為L的導體所損耗的功率。
5-13 將下列場矢量的瞬時值與復數值相互表示:
(1) 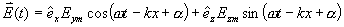
(2) 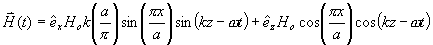
(3)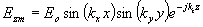
(4) 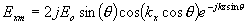
5-14 一振幅為50V/m,頻率為1GHz的電場存在于相對介電常數為2.5,損耗角正切為0.001的有耗電介質中,求每立方米媒質中消耗的平均功率。
5-15 已知無源、自由空間中的電場強度矢量
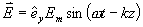
(1)由麥克斯韋方程求磁場強度,
(2)證明 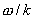 等于光速, 等于光速,
(3)求坡印廷矢量的時間平均值。
5-16 已知真空中電場強度
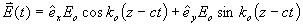
式中 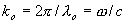 。試求:(1)
磁場強度和坡印廷矢量的瞬時值;(2) 對于給定的z值(例如z=0),試確定 。試求:(1)
磁場強度和坡印廷矢量的瞬時值;(2) 對于給定的z值(例如z=0),試確定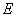 隨時間變化的軌跡;(3) 磁場能量密度,電場能量密度和坡印廷矢量的時間平均值。
隨時間變化的軌跡;(3) 磁場能量密度,電場能量密度和坡印廷矢量的時間平均值。
5-17 設真空中同時存在兩個正弦電磁場,其電場強度分別為

試證明總的平均功率流密度等于兩個正弦電磁場的平均功率流密度之和。
5-18 證明真空中無源區域的:
(1) 麥克斯韋方程組;
(2) 坡印廷矢量;
(3) 能量密度在下列變換
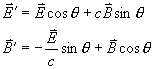
下不變。其中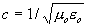 ,θ為任意的恒定角度。
,θ為任意的恒定角度。
5-19 證明均勻、線性、各向同性的導體媒質中,無源區域的正弦電磁場滿足波動方程:
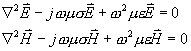
5-20 證明有源區域內電場強度矢量E和磁場強度矢量H滿足有源波動方程:
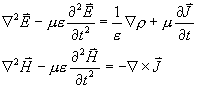
5-21 在麥克斯韋方程中,若忽略 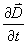 或 或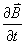 ,證明矢量位和標量位滿足泊松方程:
,證明矢量位和標量位滿足泊松方程:
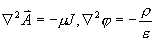
5-22 證明洛侖茲條件和電流連續方程是等效的。
|